| | |
 | SchraubTec Barcelona - Die regionale Fachmesse für Schraubverbindungen, eine Veranstaltung am 21.05.2026
|
|
Autor
|
Thema: Drehmoment für Kreisbewegung (2588 / mal gelesen)
|
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 12. Aug. 2016 21:04
erstellt am: 12. Aug. 2016 21:04  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Hallo zusammen! Bezüglich der Auslegung des erforderlichen Drehmoments für eine Kreisbewegung habe ich eine Frage: Welche Länge wähle ich als Hebelarm, wenn die Stange nicht im Körperschwerpunkt sitzt? Ich habe den Schwerpunkt berechnet und daraufhin die Abstand zur Drehachse. Die nötige Kraft kenne ich bereits. Jedoch setzt diese aussen am Körper an, sodass er in Rotation versetzt werden würde. Die Verbindung ist aber völlig starr. Habe ich dadurch Verluste beim Drehmoment? Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
ThoMay
Ehrenmitglied V.I.P. h.c.
Konstrukteur

   Beiträge: 5260
Registriert: 15.04.2007 SWX 2019
Windows 10 x64
|

 erstellt am: 13. Aug. 2016 00:07
erstellt am: 13. Aug. 2016 00:07  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
|
N.Lesch
Ehrenmitglied V.I.P. h.c.
Dipl. Ing.
     
   Beiträge: 5249
Registriert: 05.12.2005
|

 erstellt am: 13. Aug. 2016 07:01
erstellt am: 13. Aug. 2016 07:01  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
|
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 13. Aug. 2016 18:00
erstellt am: 13. Aug. 2016 18:00  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Danke für die Begrüßung! Bild wird schierig, aber ich versuchs mal ausreichend gut zu beschreiben: Der Körper wird um seine Drehachse rotiert. Er stellt näherungsweise einen Quader da. Angetrieben wird er über eine Stange. Ein Ende der Stange befindet sich im Drehzentrum und ist dort gelagert. Das andere wird an den Körper geflanscht. Nun zum Problem: Die Stange wird an der Außenseite des Körpers geflanscht. Dadurch entsteht ein Abstand zwischen Schwerpunkt und dem Punkt, an dem angeflanscht wird. Auch gibt es eine Höhendifferenz. Ich Frage mich, ob ich dadurch Verluste des Drehmoments zu befürchten habe. Wenn eine Kraft ausserhalb des Schwerpunkts angreif, verursacht sie zusätzlich Rotation. Die Verbindung ist aber völlig steif, sodass sich nichts drehen kann. Der Steinersche Satz ist eine Idee. Jedoch ist das Gewicht der Stange quasi zu vernachlässigen und würde somit kaum den Schwerpunkt beeinflussen. Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
N.Lesch
Ehrenmitglied V.I.P. h.c.
Dipl. Ing.
     
   Beiträge: 5249
Registriert: 05.12.2005 WF 4
|

 erstellt am: 13. Aug. 2016 19:57
erstellt am: 13. Aug. 2016 19:57  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
|
Roland Schröder
Ehrenmitglied V.I.P. h.c.
Dr.-Ing. Maschinenbau, Entwicklung & Konstruktion von Spezialmaschinen

   Beiträge: 13713
Registriert: 02.04.2004 Autodesk Inventor
|

 erstellt am: 14. Aug. 2016 17:29
erstellt am: 14. Aug. 2016 17:29  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Moin! Das von einer Kraft erzeugte Drehmoment bezieht sich immer auf einen bestimmten Punkt. Die Größe dieses Drehmomentes bestimmt sich allein aus dem Abstand der Kraftwirkungslinie von diesem Punkt (und natürlich der Größe der Kraft). Wie die mechanische Verbindung zu dem Kraftangriffspunkt aussieht, ist (solange man Verbiegung und so was außen vor lässt) völlig egal. ------------------
Roland
www.Das-Entwicklungsbuero.de It's not the hammer - it's the way you hit! Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
N.Lesch
Ehrenmitglied V.I.P. h.c.
Dipl. Ing.
     
   Beiträge: 5249
Registriert: 05.12.2005
|

 erstellt am: 14. Aug. 2016 18:25
erstellt am: 14. Aug. 2016 18:25  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
|
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 15. Aug. 2016 00:22
erstellt am: 15. Aug. 2016 00:22  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Das Problem ist in meinen Augen der Kraftangriffspunkt. Zur Vereinfachung reduziere ich den Körper in einen Massepunkt. Dieser Punkt ist in seinem Schwerpunkt und ich habe ihn bereits errechnet. Geometriebeding kann die Stange nicht im Massepunkt montiert werden, ansonsten würde sich das erforderliche Drehmoment aus dem Abstand des Massepunkts zur Drehachse und der erforderlichen Kraft ergeben. Nun greift die Kraft jedoch an der Aussenseite des Körpers an. Meine Bedenken ausformuliert: Energie kann nur umgewandelt werden. Es steht eine bestimmte Menge an Energie zur Verfügung, um den Körper um die Achse zu bewegen. Durch den Montageort der Stange greift die Kraft nicht im Körper Schwerpunkt an. Würde es sich um keine feste Verbindung handeln, würde sich der Körper noch zusätzlich um eine körperinterne Achse drehen. Das heißt, ein Teil der Energie geht für diese Drehung verloren. Eventuell sind meine Bedenken auch völlig unbegründet, was meint ihr? Entstehen dadurch Verluste? Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
Roland Schröder
Ehrenmitglied V.I.P. h.c.
Dr.-Ing. Maschinenbau, Entwicklung & Konstruktion von Spezialmaschinen

   Beiträge: 13713
Registriert: 02.04.2004 Autodesk Inventor
|

 erstellt am: 15. Aug. 2016 01:07
erstellt am: 15. Aug. 2016 01:07  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
|
N.Lesch
Ehrenmitglied V.I.P. h.c.
Dipl. Ing.
     
   Beiträge: 5249
Registriert: 05.12.2005
|

 erstellt am: 15. Aug. 2016 06:39
erstellt am: 15. Aug. 2016 06:39  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
|
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 15. Aug. 2016 09:54
erstellt am: 15. Aug. 2016 09:54  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
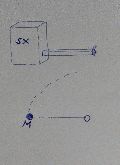
Die Masse spielt nur bei der Beschleunigung eine Rolle. Kein Magnetismus. Ich habe wohl etwas für Verwirrung gesorgt. Ich habe eine kleine Zeichnung beigefügt, evtl macht sie es klarer. Der Körper soll im Kreis bewegt werden. Dazu ist eine Stange an diesen geflanscht. S bezeichnet dabei den Schwerpunkt (das X markiert diesen). Ich möchte das Drehmoment wissen, um ihn ausreichend auf eine bestimmte Geschwindigkeit beschleunigen zu können. Das Problem kann man als Rotation oder Translastion angehen, wobei ich Translation vorziehe. Die benötige Kraft kenne ich bereits. Das bedeutet, mir fehlt für das erforderliche Drehmoment nur noch eine Strecke. Wäre es einfach ein Massepunkt, wie in der Zeichnung darunter, wäre es einfach der Abstand zwischen dem Massepunkt und der Drehachse, sprich der Radius des Kreises, den der Körper abfährt. Nun hat der Körper aber ein Volumen und die Stange ist nicht im Schwerpunkt. Bislang habe ich den Schwerpunkt errechnet und das Problem als "Massepunkt" betrachtet und so das Drehmoment bestimmt. Habe ich dadurch Verluste zu befürchten, weil die Stange nicht im Schwerpunkt sitzt? Sie kann aber als steif angenommen werden. Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 16. Aug. 2016 00:16
erstellt am: 16. Aug. 2016 00:16  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
|
N.Lesch
Ehrenmitglied V.I.P. h.c.
Dipl. Ing.
     
   Beiträge: 5249
Registriert: 05.12.2005 WF 4
|

 erstellt am: 16. Aug. 2016 06:59
erstellt am: 16. Aug. 2016 06:59  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
|
Andy-UP
Moderator
Projektingenieur
      

   Beiträge: 2567
Registriert: 27.10.2003
|

 erstellt am: 16. Aug. 2016 08:17
erstellt am: 16. Aug. 2016 08:17  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Hallo KuchenFreund, Wie Roland weiter oben schon geschrieben hat, gilt für die Berechnung der Beschleunigung der Abstand zwischen Drehachse und Schwerpunkt des Körpers. Die Lage und Ausführung deines Hebels spielt aber sehr wohl eine Rolle bei der Berechnung desselben. Bei einer Ausführung gemäss deiner Skizze würde durch die Fliehkraft ein Biegemoment und bei Beschleunigung bzw. Verzögerung ein Torsionsmoment erzeugt. Ob in deinem Fall relevante Momente erzeugt werden kann ich ohne Angaben wie Beschleunigung, Masse, Abstand zur Rotationsachse, Abstand Masseschwerpunkt - Hebel, Winkelgeschwindigkeit nicht sagen. Ciao Andreas Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 16. Aug. 2016 11:09
erstellt am: 16. Aug. 2016 11:09  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Danke, das ist in etwa worauf ich hinaus wollte. Ich drücke mich manchmal unglücklich aus. Natürlich brauche ich nur für die Beschleunigung das Drehmoment, schließlich habe ich so die Kraft errechnet, um den Körper auf die definierte Geschwindigkeit zu bringen. Ich war mich nicht ganz im klaren, ob trotz einer annehmbaren steifen Verbindung Momente entstehen, schließlich greift die Kraft nicht im Schwerpunkt an. Die Richtung dieser entstehenden Momente zeigt entgegengesetzt zu dem Moment, das den Antrieb verursacht. Ich habe mich gefragt, ob ich dadurch Antriebsverluste erleide. Natürlich entstehen Momente, jedoch haben diese aufgrund der steifen Verbindung "keinen visuellen Einfluss". Gibt es dennoch einen rechnerischen? Dann wären wir auch wieder bei meinem Energie-Statement: Wenn ich die Rotationsenergie nicht nur dazu verwende den Körper im Kreis zu bewegen, sondern ebenfalls ein Teil dafür aufgewandt wird ihn in Rotation zu versetzen, dann kann ich nicht dieselbe Beschleunigung erwarten, oder täusche ich mich? Sonst müsste ich Energie aus dem nichts schaffen. Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
Roland Schröder
Ehrenmitglied V.I.P. h.c.
Dr.-Ing. Maschinenbau, Entwicklung & Konstruktion von Spezialmaschinen

   Beiträge: 13713
Registriert: 02.04.2004 Autodesk Inventor
|

 erstellt am: 16. Aug. 2016 12:30
erstellt am: 16. Aug. 2016 12:30  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Zitat:
Original erstellt von KuchenFreund:
Energie ... nicht nur dazu verwende den Körper im Kreis zu bewegen, sondern ebenfalls ein Teil dafür aufgewandt wird ihn in Rotation zu versetzen, ...
Das ist richtig überlegt! Zum einen muss Dein "Massepunkt" auf eine bestimmten Geschwindigkeit auf der Kreisbahn gebracht werden, zum Anderen rotiert Dein Körper dann, und muss gleichzeitig mit auf diese Eigenrotation beschleunigt werden. Da aber bei diesen Betrachtungen der Abstand vom Drehzentrum quadratisch eingeht, ist die Energie bzw. Beschleunigung für die Kreisbahn meistens sehr viel größer als jene für die Eigenrotation. ------------------
Roland
www.Das-Entwicklungsbuero.de It's not the hammer - it's the way you hit! Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
ulrix
Mitglied
Maschinenbauingenieur
  
   Beiträge: 742
Registriert: 10.07.2007 Core 2 Duo 2,13 GHz / 2GB RAM
GeForce 7900 / 256 MB
Space Navigator
XP Pro SP2
AIS 2010
|

 erstellt am: 16. Aug. 2016 13:46
erstellt am: 16. Aug. 2016 13:46  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Zitat:
Original erstellt von KuchenFreund:
Das Problem kann man als Rotation oder Translastion angehen, wobei ich Translation vorziehe.
Und das ist meines Erachtens nicht richtig überlegt. Um beide Anteile zu berücksichtigen, nämlich die Bewegung des Körpers auf einer Kreisbahn und die Rotation des Körpers um seine Achse, sollte man diesen Fall als Rotationsbewegung betrachten.
Das Massenträgheitsmoment ist dann, wie bereits erwähnt, nach dem Steinerschen Satz zu berechnen. Wenn man unbedingt will, kann man diesen Fall wohl auch als kombinierte Translation / Rotation auffassen, was mir aber umständlicher erscheint.
Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 16. Aug. 2016 14:33
erstellt am: 16. Aug. 2016 14:33  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Zitat:
Zum einen muss Dein "Massepunkt" auf eine bestimmten Geschwindigkeit auf der Kreisbahn gebracht werden, zum Anderen rotiert Dein Körper dann, und muss gleichzeitig mit auf diese Eigenrotation beschleunigt werden. Da aber bei diesen Betrachtungen der Abstand vom Drehzentrum quadratisch eingeht, ist die Energie bzw. Beschleunigung für die Kreisbahn meistens sehr viel größer als jene für die Eigenrotatio
Das habe ich mir gedacht, jedoch kann der Körper nicht rotieren, da er ja befestigt ist. Ich frage mich, ob ich da auch noch von "Verlusten" sprechen kann, schließlich wird die Rotation verhindert. Sicherlich ist es auch mit dem Trägheitsmoment berechenbar und bietet sich auch an. Ich ziehe dennoch Translation vor, weil ich es mir besser vorstellen kann. Der Punkt, auf den ich hinausmöchte, ist, dass der Körper keine Rotation ausüben kann, da er steif an der Stange befestigt ist. Ich Frage mich, ob das dennoch zu einem Verlust bei der Beschleunigung führt. Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
Roland Schröder
Ehrenmitglied V.I.P. h.c.
Dr.-Ing. Maschinenbau, Entwicklung & Konstruktion von Spezialmaschinen

   Beiträge: 13713
Registriert: 02.04.2004 Autodesk Inventor
|

 erstellt am: 16. Aug. 2016 14:42
erstellt am: 16. Aug. 2016 14:42  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Zitat:
Original erstellt von KuchenFreund:
..., dass der Körper keine Rotation ausüben kann, da er steif an der Stange befestigt ist.
Nein, er muss rotieren, weil bzw. wenn er an der Stange befestigt ist. Bei jeder Umdrehung der Stange muss er sich ein Mal mitdrehen, wie die kleinen Autos in einem einfachen Karussel. Das Gegenteil wäre z. B. das Riesenrad; da drehen sich die Kabinen nicht mit, sondern zeigen immer in dieselbe Richtung (Boden nach unten). ------------------
Roland
www.Das-Entwicklungsbuero.de It's not the hammer - it's the way you hit! Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 16. Aug. 2016 16:34
erstellt am: 16. Aug. 2016 16:34  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Das verstehe ich nicht ganz. Die Stange ist an den Körper angeflanscht, wenn der Körper rotieren können würde, müsste er somit die ganze Stange um sich herum verbiegen. Zum Vorstellen: Ich stecke einen Marshmallow an einen dünnen Stock und drehe mich selbst im Kreis. Der Marshmalow roiert mit, aber nicht um seine eigene Achse. Der Stock steckt nur ganz am Rand des Marshmmallows. Und die Stirnseite des Marshmallows zeigt immer in das Zentrum der Drehbewegung. Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
Torsten Niemeier
Ehrenmitglied V.I.P. h.c.
Maschinenbau Ingenieur

   Beiträge: 3890
Registriert: 21.06.2001 "ZUSE I.36", 8 BIT, 32 Lämpchen, Service-Ölkännchen "ESSO-Super", Software: AO auf Kuhlmann-Parallelogramm-Plattform
** CSWP 04/2011 **
** CSWE 08/2011 **
|

 erstellt am: 16. Aug. 2016 16:43
erstellt am: 16. Aug. 2016 16:43  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Ich verstehe den Fred hier immer weniger. Es wird einfach nur ein Körper um eine Achse gedreht, und Du meinst, weil die Stangenachse nicht durch den Schwerpunkt des Körpers geht würde das etwas an dem erforderlichen Beschleunigungsmoment ändern? Häh?
Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
ulrix
Mitglied
Maschinenbauingenieur
  
   Beiträge: 742
Registriert: 10.07.2007 Core 2 Duo 2,13 GHz / 2GB RAM
GeForce 7900 / 256 MB
Space Navigator
XP Pro SP2
AIS 2010
|

 erstellt am: 16. Aug. 2016 18:38
erstellt am: 16. Aug. 2016 18:38  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Zitat:
Original erstellt von KuchenFreund:
Und die Stirnseite des Marshmallows zeigt immer in das Zentrum der Drehbewegung.
Das ist richtig.
Und das Zentrum der Drehbewegung ist mal oberhalb und mal unterhalb des Marshmallows (bei waagerechter Rotationsachse)
bzw. mal nördlich und mal südlich vom Marshmallow (bei senkrechter Rotationsachse) Das alles passt nur zusammen, wenn der Marshmallow sich dreht. Wie soll denn der (am Marshmallow fixierte) Zahnstocher mal nach oben und mal nach unten zeigen, ohne dass der Marshmallow sich dreht?
Vielleicht solltest Du noch mal intensiv über den Vergleich Karussell - Riesenrad nachdenken. Noch anschaulicher kann man es eigentlich nicht erklären. Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 16. Aug. 2016 23:07
erstellt am: 16. Aug. 2016 23:07  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Ich habe etwas den Faden verloren. Wieso zeigt der Zahnstocher mal nach oben und mal nach unten? Er ist in der mitte drehbar fixiert und somit kann er sich nur um Kreis drehen. Diese Fixierung stellt auch das Zentrum der Drehbewegung dar, sie ist somit ortsfest. Wenn ich mich im Kreis drehe und den Marshmallow mit Zahnstocher von mir wegstrecke, so dreht er sich nicht um seine eigene Achse, sonder macht eine Kreisbewegung um meine Achse. Für eine Rotation um seine Achse müsste sich der Zahnstocher verbiegen. Ich schaue somit immer diesselbe Seite des Marshmallows an.
Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
ulrix
Mitglied
Maschinenbauingenieur
  
   Beiträge: 742
Registriert: 10.07.2007 Core 2 Duo 2,13 GHz / 2GB RAM
GeForce 7900 / 256 MB
Space Navigator
XP Pro SP2
AIS 2010
|

 erstellt am: 17. Aug. 2016 07:42
erstellt am: 17. Aug. 2016 07:42  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Dann such Dir mal einen Helfer, der sich ganz still in 5m Abstand auf einen Stuhl setzt und Dich mit dem Marshmallow beobachtet. Wenn Du Dich mitsamt dem Marshmallow drehst, sieht der Helfer dann auch immer dieselbe Seite des Marshmallows? Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
bacengeugn
Mitglied
Konstrukteur
 
   Beiträge: 181
Registriert: 10.11.2011
|

 erstellt am: 17. Aug. 2016 09:48
erstellt am: 17. Aug. 2016 09:48  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Antriebsverluste würdest du beim Beschleunigen erleiden in Form von Potentieller Energie im Biegebalken. Also rechne
-
Rotationsbeschleunigungsarbeit Rotationsenergie bei Endgeschwindigkeit
- + Verformungsarbeit des Biegebalkens:
(Fliehkraft, die nach der Beschleunigung auftritt) * (Abstand zwischen Schwerpunkt und Stabbefestigung) = Biegemoment, das Biegemoment brauchst du dann zur Potentialberechnung
- daraus kannst du dein Drehmoment zur Beschleunigung berechnen (Beschleunigungsarbeit). Dafür Trägheitsmoment von Quader und Stab bezüglich der Rotationsachse bestimmen
Anmerkung: In diesem Link - Gleichung 4, erster Term für das Potential des Balkens verwenden. [EDIT] hatte den Link falsch eingetragen Zur Rotation des Quaders:
Wenn du dich in der Mitte der Drehachse mitdrehst dann scheint der Quader für dich nicht zu rotieren, aber DU rotierst. Wenn du dich daneben stellst dann scheint sich der Quader zu rotieren, denke dir den Stab weg und fixiere deinen Blick auf einem Punkt des Quaders während er sich auf seiner Kreisbahn befindet -> Er rotiert. PS: Sag mir anschließend bitte ob wirklich ein nennenswerter Unterschied herauskommt durch die Berücksichtigung der Verformung  [Diese Nachricht wurde von bacengeugn am 17. Aug. 2016 editiert.] [Diese Nachricht wurde von bacengeugn am 17. Aug. 2016 editiert.] [Diese Nachricht wurde von bacengeugn am 17. Aug. 2016 editiert.] Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 17. Aug. 2016 11:30
erstellt am: 17. Aug. 2016 11:30  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Code:
Dann such Dir mal einen Helfer, der sich ganz still in 5m Abstand auf einen Stuhl setzt und Dich mit dem Marshmallow beobachtet.
Wenn Du Dich mitsamt dem Marshmallow drehst, sieht der Helfer dann auch immer dieselbe Seite des Marshmallows?
Natürlich nicht, aber es geht doch um die Sicht aus meiner Richtung und nicht um die eines externen Beobachters. Ich verstehe zumindest den Zusammenhang nicht ganz. Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 17. Aug. 2016 11:39
erstellt am: 17. Aug. 2016 11:39  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Hallo bacengeun, dein Link bringt mich leider zu keinem PDF-Dokument. Eventuell habe ich darauf keinen Zugriff. Da die Bewegung langsam ablaufen wird, kann man direkt sagen, dass die Fliehkraft und die Biegung quasi zu vernachlässigen sind. Aber ich denke, ich kann nun mein Problem zusammenfassen: Das benötigte Drehmoment errechnet sich aus der benötigten Kraft, den Körper auf eine bestimmte Geschwindigkeit zu beschleunigen und aus dem Abstand Schwerpunkt des Körpers zur Rotationsachse. Da die Stange nicht im Schwerpunkt ansetzt, entstehen Verluste durch Biegung, die aus dem dezentralen Kraftangriffpunkt resultiert --> Moment und natürlich der Fliehkraft, da es sich um eine Kreisbewegung handelt. Diese sollte bei genauen Berechnungen berücksichtigt werden. In meinem Fall ist die Beschleunigung gering und ich habe bereits gesagt, dass die Stange deswegen als vollkommen starr angenommen werden kann. Vielen Dank für eure Hilfe! Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
ulrix
Mitglied
Maschinenbauingenieur
  
   Beiträge: 742
Registriert: 10.07.2007 Core 2 Duo 2,13 GHz / 2GB RAM
GeForce 7900 / 256 MB
Space Navigator
XP Pro SP2
AIS 2010
|

 erstellt am: 17. Aug. 2016 11:51
erstellt am: 17. Aug. 2016 11:51  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Zitat:
Original erstellt von KuchenFreund:Natürlich nicht, aber es geht doch um die Sicht aus meiner Richtung und nicht um die eines externen Beobachters.
Das ist der Irrtum.
Aus Deiner Sicht drehst Du Dich ja gar nicht und vor allem der Marshmallow bewegt sich aus Deiner Sicht überhaupt nicht, geschweige denn auf einer Kreisbahn. Aus Deiner Sicht dreht sich die ganze Welt (mit Ausnahme des Marshmallows) sich um Dich herum.
Diese Betrachtungsweise ist zwar in sich korrekt, aber sie ergibt keine sinnvollen Ergebnisse in Bezug auf den Zusammenhang zwischen Drehmoment und Winkelbeschleunigung. Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
bacengeugn
Mitglied
Konstrukteur
 
   Beiträge: 181
Registriert: 10.11.2011
|

 erstellt am: 17. Aug. 2016 12:31
erstellt am: 17. Aug. 2016 12:31  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
Ich hatte die URL an der falschen Stelle eingetragen. Jetzt gehts. Die Fliehkraft wirkt an sich nicht dem Antriebsmoment engtegen, erst durch die Biegung die sie erzeugt. Aber wichtiger ist es wahrscheinlich die Reibung in der Lagerung zu berücksichtigen. [Diese Nachricht wurde von bacengeugn am 17. Aug. 2016 editiert.] Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 17. Aug. 2016 12:42
erstellt am: 17. Aug. 2016 12:42  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Ah, jetzt habe ich es begriffen, danke ulrix! Mir ging es um das Verständnis, ob theoretisch weitere Erscheinungen auftrenen können. Ich werde weiter so vorgehen, wie gehabt und den Schwerpunkt berechnen und daüber das Moment. Die Folgeerscheinungen durch des nicht im Schwerpunkt anflaschen sind mit Sicherheit so klein, dass sie zu vernachlässigen sind. Danke nochmal für eure Hilfe! Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
ccmpe20
Mitglied
Maschinenbauingenieur / Allrounder
 
   Beiträge: 201
Registriert: 16.06.2009 HP ZBook 17 G4 Mobile Workstation
Windows 10 Pro 64
Intel Core i7-7820HQ NVIDIA Quadro P3000
Creo Elements/Direct 19
daheim: PE6
|

 erstellt am: 17. Aug. 2016 13:00
erstellt am: 17. Aug. 2016 13:00  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:           Nur für KuchenFreund Nur für KuchenFreund 
|
KuchenFreund
Mitglied

   Beiträge: 16
Registriert: 20.07.2016
|

 erstellt am: 18. Aug. 2016 00:48
erstellt am: 18. Aug. 2016 00:48  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Danke für die Literatur! Du hast recht, meine Ausdrucksweise ist nicht immer vorteilhaft. Eine detailierte Skizze wäre mit Sicherheit angebracht.Ich werde daran denken, falls ich mal wieder eine Frage in diesem Forum stelle. Aber vielen Dank für die große Teilnahme an der Diskussion. Es hat mich gefreut und gleichzeitig erstaunt, dass mir so viele Menschen ihre Hilfe angeboten haben, vielen Dank! Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |

 Foren auf CAD.de
Foren auf CAD.de

 Mechanische Antriebstechnik
Mechanische Antriebstechnik

 Drehmoment für Kreisbewegung
Drehmoment für Kreisbewegung

![]()





























 .
.