|
Autor
|
Thema: Der Cylindro-Pentagon-Dodekaeder (12626 mal gelesen)
|
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002 C 64
Amiga 1000 mit
8.5 MB RAM und
Seagate ST225
RLL formatiert
|

 erstellt am: 09. Feb. 2010 00:27
erstellt am: 09. Feb. 2010 00:27  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
|
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002
|

 erstellt am: 09. Feb. 2010 00:31
erstellt am: 09. Feb. 2010 00:31  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
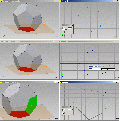
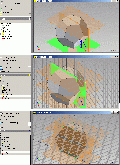
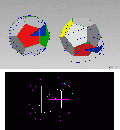
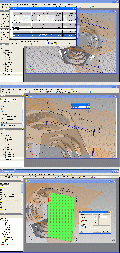
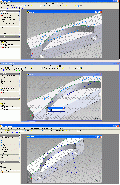
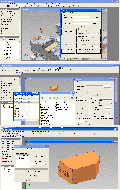
1. Die Konstruktion des Dodekaeders mit InventorIn diesen Bilderserien ist bis Pic10 jeweils links der fertige Dodekaeder zu sehen, rechts die Konstruktionsschritte, so daß diese am fertigen Modell nachvollzogen werden können. Bild 01 – oben: Wir beginnen mit der Grundfläche, am Fertigmodell rot eingefärbt, das Zentrum des Umkreises wird auf den Koordinatenusprung von Inventor gelegt. Wir skizzieren auf den Ursprung ein Fünfeck. Bild 01 – Mitte:
Nun werden die Abhängigkeiten vergeben, das Zentrum fixiert, die rechte Linie wird auf VERTIKAL gesetzt und das einzige Maß für den Grundkörper angetragen, die Kantenlänge, sie soll hier 50mm betragen. Bild 01 unten: Wie groß ist nun der Flächenwinkel? Von mehreren Konstruktionsmöglichkeiten wählen wir hier eine einfache, so als ob wir den Dodekaeder aus einer Papierabwicklung falten würden. Wir brauchen dazu zunächst nur ein Fünfeck, skizzieren es, es wird im Fertigmodell die Stelle des grünen einnehmen.
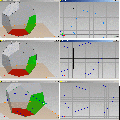
Bild 02 – oben:
Um dieses zweite Fünfeck an das erste zu binden, wird eine Ecke des noch freien Fünfecks an das untere Ende der vertikalen Linie mit Abhängigkeiten gebunden. Bild 02 – Mitte: Ebenso die zugehörige zweite Ecke des losen Fünfecks, mit dem Vergeben der zwei Punktabhängigkeiten ist das zweite Fünfeck in Lage und Größe festgelegt, aber es liegt noch in der Grundebene. Bild 02 – Unten: Jetzt wird ein wenig vorgegriffen, um das Prinzip zu zeigen. Am Fertigmodell wurden an den unteren fünf, schrägstehenden Fünfecken jeweils eine waagrechte Linie eingezeichnet, von Ecke zu Ecke, parallel zur Faltlinie ganz unten. Ebenso zwei Mittellinien, einmal am roten, einmal am grünen Fünfeck. Pic 03 – oben: Nun schauen wir von unten auf das Fertigmodell. Die beiden Mittellinien bilden eine gerade Linie und die Eckenverbindungslinien bilden wieder ein Fünfeck, dessen Kantenlänge aber bekannt ist, sie entspricht dem Abstand zweier gegenüberliegender Ecken. Pic 03 – Mitte. Man braucht also nur diese Eckenverbindung am noch liegenden Skizzenfünfeck einzuzeichnen und ebenso die Mittelinie zur Faltkante und das liegende Fünfeck hochzuklappe, bis es mit der umlaufenden Verbindungslinie zur Deckung kommt. Nun geht’s rechts in den Skizzen wieder weiter. Pic 03 – unten: Also zeichnen wir in der Skizze ins rechte Fünfeck zuerst die Verbindungslinie von der oberen zur unteren Ecke ein und die Verbindungslinie von der Mitte der zu beiden Fünfecken gehörenden Kante zur Mitte der soeben gezeichneten Eckverbindungslinie.
------------------
-
Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002 C 64
Amiga 1000 mit
8.5 MB RAM und
Seagate ST225
RLL formatiert
|

 erstellt am: 09. Feb. 2010 00:36
erstellt am: 09. Feb. 2010 00:36  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
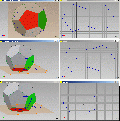
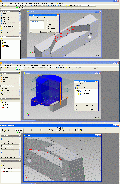
Pic 04 – oben Das große Fünfeck, das von den umlaufenden Verbindungslinien gebildet wird, zeichnen wir jetzt in den Grundriss, das Zentrum wieder in den Ursprung. Bild 04 – Mitte: Mit Abhängigkeiten richten wir es aus, daß die gleiche Orientierung, die Kantenlänge kann von der Eckenverbindungslinie des rechten Fünfecke übernommen werden. Bild 04 – unten: Damit ist die erste Skizze auf der XY-Ebene vorläufig fertig, nun brauchen wir eine senkrechte dazu, die Ursprungsebene XZ wird sichtbar geschaltet und eine Skizze darauf gelegt. Bild 05 – oben: Um von dieser Skizze auf Geometrie der vorheringen zugreifen zu können, müssen die grün dargestellten Linien in die Skizze projiziert werden. Bild 05 – Mitte: Eine Senkrechte nach oben von der Projektion der Seitenkante des großen Fünfecks, auf dieser vertikalen Linie liegt der gesucht Punkt. Bild 05 – unten: Nun noch ein Kreis auf der Projektion der Faltkante, also der gemeinsamen Kante der beiden kleinen Fünfecke. Dieser Kreis schneidet die gerade gezeichnete Linie.
Bild 06 – oben:
Nun kann die vertikale Linie ggf. gedehnt werden oder alles gestutzt, so daß nur noch die benötigten Linien übrig bleiben. Zudem zeichnen wir eine Linie vom oberen Ende des Kreisbogens zu seinem Zentrum, sie liegt auf dem schrägen, im linken Bild grün dargestellten Fünfeck und mit ihr haben wir den gesuchten Flächenwinkel. Bild 06 – Mitte: Beim Dodekaeder liegen sich immer zwei Fünfecke parallel gegenüber, nur die Orientierung der Fünfecke ist um 180 Grad gedreht, wir können also auch gleich diese Flächenlinie skizzieren, sie führt uns auch zur Höhe des Dodekaeders. Im fertigen Modell links ist diese Fläche gelb, die rote wäre unten, die grüne hinten. Bild 06-unten. Die untere Ecke des gelben Fünfecks liegt auf dem umlaufend eingezeichneten Fünfeck und damit auf der gerade ermittelten Höhe. Wir brauchen in unseren Skizzen also nur eine horizontale Linie nach hinten zu ziehen. Auch die Lage ist schon bekannt, man braucht nur von der hinteren Ecke des großen Fünfecks nach oben zu gehen, der Schnittpunkt beider Linien ist die gesuchte Ecke des Fünfecks. ------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002
|

 erstellt am: 09. Feb. 2010 00:40
erstellt am: 09. Feb. 2010 00:40  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
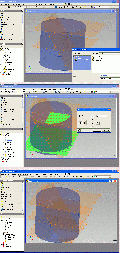
Pic 07 – oben: Da die Flächenrichtung jetzt bekannt ist, braucht vom eben ermittelten Eckpunkt nur eine Linie skizziert werden, die parallel zur vorherigen Flächelinie (des grünen Fünfeckes) verläuft. Die Abhängigkeit Parallel wird vergeben. Pic 07 – Mitte: Die Länge dieser Linie geht von der Mitte einer Fünfeckseite zur gegenüberligenden Ecke, wir holen sie uns vom allerersten Fünfeck, skizzieren sie dort ein und übertragen die Länge mit der Abhängigkeit GLEICH an Mittellinie für das gelbe Fünfeck. Mit ihrem Ende kennen wir jetzt auch die Höhe des Dodekaeders. Pic 07 – unten: Eine Arbeitsebene parallel zur XY-Ebene durch den oberen Punkt wird erstellt.
Pic 08 – oben
Wir kehren kurz noch in die erste XY-Skizze zurück, skizzieren um das große Fünfeck einen Umrkeis und verlassen die Skizze wieder, der Kreis dient zur Modellierung des umschließenden Zylinders. Pic 08 – Mitte: Wählen den vollen Grundkreis als Extrusionsfläche und die Ausführung bis zur oberen Ebene. Pic 08 – unten: und extrudieren den Zylinder. Pic 09 – oben: Da die Auswahl der Extrusionsflächen auf der XZ-Ebene nicht einfach ist, erstellen wir hier nochmal eine Skizze, projizieren die Aussenkanten des Zylinders und die beiden schrägen Linien, die rechts unten müssen wir noch bis zur Zylinderaussenkante verlängern. Pic 09 – Mitte: Und führen die Extrusion als Differenz nach beiden Seiten durchgehend aus.
Pic 09 - unten
Man erhält die ersten beiden schrägen Flächen. Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002 C 64
Amiga 1000 mit
8.5 MB RAM und
Seagate ST225
RLL formatiert
|

 erstellt am: 09. Feb. 2010 00:44
erstellt am: 09. Feb. 2010 00:44  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
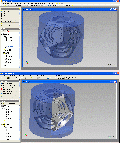
Pic 10 oben: Abschließend machen wir eine runde Anordnung dieser beiden Flächen, fünfmal um die Z-Achse. Pic 10 – unten: Und erhalten den Dodekaeder-Grundkörper. Zur Sicherheit sollte man ein paar Kanten nachmessen.
Pic 11 – oben
Zuerst erstellen wir uns eine Arbeitsebene auf halber Höhe, klicken also die untere Ebene und einen mittleren Punkt auf einer der Kanten in der Mitte. Pic 11 – Mitte: Wir wählen die senkrechte Urspungsebene und setzen eine Skizzierebene darauf und kappen das Teil. Pic 11 – unten: Wir projizieren uns die Z-Achse, die Arbeitsebene auf mittlerer Höhe sowie alle Kanten des oberen und unteren Fünfecks in die Skizze. Zudem brauchen wir noch eine der oberen Kanten des Fünfecks links oben. Pic 12 – oben: Wir ziehen eine Diagonale, von links oben nach rechts unten. Pic 12 – Mitte: Nun vom Schnittpunkt der Diagonalen mit der Projektion der Z-Achse zwei Linien, eine oberhalb der Diagonalen, eine unterhalb, dehnen oder stutzen sie ggf. auf die Kanten, bemaßen sie. Die hier angegebenen Maße könne also auch geändert werden. Ebenso ist nicht zwingend, daß die Linien exakt den Mittelpunkt treffen, dies beeinflusst das spätere Design, man kann es mit wenigen Bemaßungen steuern. Pic 12 – unten Wir tragen die Stufenlinie an, fangen oben auf der inneren Linie an, senkrecht nach unten bis zur äusseren Linie, dann wieder waagrecht zur inneren usw. Hier muß man sicher mit Abhängigkeiten noch dafür sorgen, daß die Linien wirklich so verlaufen. ------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002
|

 erstellt am: 09. Feb. 2010 00:47
erstellt am: 09. Feb. 2010 00:47  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Pic 13 – oben: Die schrägen Linien werden zu Konstruktionslinien umdefiniert, die Kontur oben und unten zur Achse hin geschlossen und eine vertikale Linie auf der senkrechten Achse gezogen, so daß sich eine geschlossene Kontur ergibt, diese läßt sich danach problemlos wählen, eine Drehung mit Differenz um die Z-Achse ausgeführt. Pic 13 – Mitte: Diese ausgeführte Drehung wird gespiegelt auf das untere Fünfeck, dazu dient jetzt die mittlere Arbeitsebene. Pic 13 – unten: Eine weitere Arbeitsebene, schräg, eine Kante des oberen Fünfecks und als zweite Kante die diagonal gegenüberliegende des unteren Fünfecks. Pic 14 – oben: Nun werden die beiden ersten Eindrehungen um diese schräge Ebene gespiegelt, man wählt also entweder die untere Eindrehung oder die Spiegelung im Browser sowie die schräge Ebene als Spiegelebene. Pic 14 – Mitte: Nun wählt man die Eindrehung an der schägen Seite, die durch die Spiegelung entstanden ist und setzt eine runde Anordnung, als Achse wieder die Z-Achse. Inventor erstellt nun die Eindrehungen an allen Seitenflächen. Gefällt das Design noch nicht, kann man es mit den Bemaßungen der beiden Steuergeraden anpassen. Damit ist das CAD-Modell des Dodekaeders erstellt und der erste Teil abgeschlossen.
------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002 C 64
Amiga 1000 mit
8.5 MB RAM und
Seagate ST225
RLL formatiert
|

 erstellt am: 14. Feb. 2010 01:21
erstellt am: 14. Feb. 2010 01:21  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
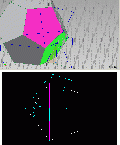
2. Die Zeichnung.
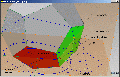
Diese Zeichnung würde von der Konstruktion an die Fertigung gegeben, normalerweise ergänzt um Material und Toleranzen.
Die beiden Ansichten links liefern Informationen vorrangig für den Materialzuschnitt, die obere Ansicht die Höhe, die untere den Durchmesser. Für die Fertigung hilft zunächst nur das Höhenmaß der oberen Ansicht, der Fertiger weiß im Regelfall jedoch nicht, daß dieses Maß das Abstandsmaß für alle parallen Flächen ist. Die Hilfsmaße in der unteren Ansicht sind zwar auf den ersten Blick schön, aber auch sie nutzen nicht viel, denn messen kann man sie kaum. Die Ansicht rechts liefert die Maße für die Eindrehungen, damit kann man etwas anfangen. Das wichtigste Maß ist der Flächenwinkel, hier absichtlich mit vielen Dezimalstellen angegeben.
Der Konstrukteur hat zwar alle Maße angegeben, mehr als nötig, doch diejenigen, die für die Programmierung der CNC-Maschine nötig wären, egal ob 3 Achsen oder mehr – sie fehlen.
Die Zeichnung hilft der Fertigung nur wenig, es muß gerechnet werden. Für einige charakteristische Größen und den Flächenwinkel soll dies im nächsten Abschnitt gemacht werden. Den CAM-Programmierer interessiert das alles nicht, er nimmt das 3d-Modell und stellt die Überlegungen zu Rohteil, Schnittaufteilung und nötige Spannhilfsmittel an. ------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002
|

 erstellt am: 03. Mrz. 2010 00:56
erstellt am: 03. Mrz. 2010 00:56  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
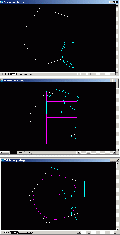
3. Was wäre wenn – wir kein CAM hätten?Dann würde die zeichnerische Genauigkeit mit CAD genügen, was aber, wenn wir nur eine Zeichnung bekommen? Einer würde rechnen müssen, entweder der Konstrukteur oder der Mitarbeiter an der Maschine. Das soll hier exemplarisch einmal gemacht werden. Sehen wir uns zunächst Pic 15 an, es wird uns durch die ganze Berechnung begleiten. Unten als Bodenfläche des Dodekaeders haben wir das rote Fünfeck, rechts daneben in seiner Ebene ist ein weiteres Fünfeck eingezeichnet, klappen wir es an der gemeinsamen Kante hoch, wird es zum grünen Fünfeck, den Kippwinkel (w) brauchen wir. Am schräg stehenden, grünen Fünfeck können wir ein rechtwinkliges Dreieck einzeichnen, es ist mit der strichpunktierten Linie markiert, zwei Seiten können berechnet werden, es ist die Hypotenuse und die am Kippwinkel anliegende Kathete, damit wird der Kippwinkel: cos (w) = k / h An h kommen wir, wenn wir das Eckenmaß e einzeichnen. Ein wenig mehr Aufwand braucht k, dazu verbinden wir die Ecken der unteren 5 schrägen Fünfecke, diese Verbindungslinie bildet wieder ein Fünfeck, das in der Ebene des roten Grundfünfecks auch einfach skizziert werden kann. Beschreibt man nun in dieses große Fünfeck und in das rote Fünfeck jeweils den Inkreis ein, so ergibt sich k als Differenz der beiden Inkreisradien. Das sollte also zu machen sein. Und jetzt alles Schritt für Schritt.
Pic 16 – oben:
Fangen wir mit dem Eckenwinkel des Fünfecks an, weil wir den zuerst brauchen. Gedanklich gehen wir jetzt einmal auf dem Fünfeck entlang, auf jeder Ecke drehen wir uns um einen konstanten Winkel. Wenn wir auf dem Ausgangspunkt ankommen, haben wir uns einmal komplett gedreht, also 360 Grad. An jeder Ecke drehen wir uns um 360 Grad / 5 = 72 Grad. Der Innenwinkel des Fünfecks ergänzt sich zu 180 Grad., der Winkel zwischen zwei Seiten beträgt also 180 Grad – 72 Grad = 108 Grad. Pic 16 – Mitte: Gehen wir die Hypotenuse an, das Maß h. Dazu verschieben wir diese Linie einfach nach oben zur nächsten Ecke, erhalten wieder ein rechtwinkliges Dreieck. Wir kennen dort die Hypotenuse, es ist die Seitenlänge des Fünfecks und den Winkel, er beträgt 180 Grad – 90 Grad = 18 Grad. Damit wird: h / s = cos (18°) und umgestellt: h = s * cos (18°)
Damit haben wir bereits die erste Seite des strichpunktierten Dreiecks aus Pic 15. Nun zur zweiten.
Pic 16 – unten: Wir zeichnen den Inkreis ein und verbinden sein Zentrum mit einer Ecke und ebenso mit der Mitte einer Seitenkante, wir bekommen wieder ein rechtwinkliges Dreieck, von dem wir eine Seite – die halbe Seitenlänge s/2 - kennen und alle Winkel. Die Verbindungslinie vom Zentrum zur Ecke halbiert die 108 Grad, dort ist der Winkel 54 Grad. Am Zentrum ist der Winkel 36 Grad. würden wir alle Ecken mit dem Inkreiszentrum verbinden, bilden die einen Winkel von 360°/5 = 72°, das Dreieck hat den halben Winkel, also 36 Grad. Damit erhalten wir: (s/2) / r = tan (36°) und umgestellt den Inkreisradius des Bodenfünfecks: r = s / (2*tan(36°))
Pic 17 – oben:
Bis jetzt haben wir also nichteinmal eine Formelsammlung bemühen müssen, das kann auch so bleiben. Nun müssen wir uns an das große Fünfeck machen, also die Projektion der Ecken. Die Seitenlänge dieses Fünfecks ist das Eckenmaß des kleinen. Also berechnen wir dieses Eckenmaß in Abhängigkeit der Kantenlänge. Wir können wieder ein rechtwinkliges Dreieck in das Fünfeck skizzieren, verbinden die obere und untere Ecke, das ist das Eckenmaß und von der linken Ecke zur Eckenmaßlinie. Damit erhalten wir: (e/2) / s = sin(54°) umgestellt: e = 2 * s * sin(54°)
Pic 17 – unten:
Nun benötigen wir noch den Inkreisradius des großen Fünfecks. Da wir oben den Bezug zur Seitenlänge im kleinen Fünfeck schon ermittelt haben, brauchen wir als Seitenlänge nur das Eckenmaß einzusetzen und erhalten: R = (2*s*sin(54°)) / (2*tan(36°)) Die 2 kürzt sich heraus, wir bekommen: R = s * sin(54°) / tan (36°)
Damit wird
R – r = s*sin(54°)/tan(36°) - s / (2*tan(36°)) Wir klammern s aus: R-r = s * (sin(54°)/tan(36°)- 1/(2*tan(36°)) Auch den tan(36°) ausklammern und nach hinten: R-r = s*((sin(54°)-0.5)/tan(36°) Und damit zurück zu Pic 15 zu dem strichpunktierten Dreieck:
cos (w) = (R-r) / h = (s*((sin(54°)-0.5)/tan(36°)) / (s*cos(18°))
s kann erwartungsgemäß gekürzt werden, der Winkel muß ja seitenlängenunabhängig sein: cos (w) = (sin(54°)-0.5) / ( cos(18°) * tan(36°)) w = 63,434948823 Grad. Der von zwei Flächen gebildete Innenwinkel ergänzt sich zu 180 Grad, ist also 116,565051177 Grad.
Ein Kunststück war das also nicht. Jetzt brauchen wir noch den Umkreisdurchmesser und den Abstand zweier parallel gegenüberliegender Fünfecke für den Materialzuschnitt, das soll im nächsten Abschnitt berechnet werden.
------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002 C 64
Amiga 1000 mit
8.5 MB RAM und
Seagate ST225
RLL formatiert
|

 erstellt am: 30. Mrz. 2010 23:57
erstellt am: 30. Mrz. 2010 23:57  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
4. Daten für den Materialzuschnitt berechnen.
Technische Zeichner sollten die Aussenmaße angeben. Manchmal tun sie es nicht, dann muß gerechnet werden. Exemplarisch sollen auch diese beiden Informationen berechnet werden.
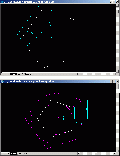
Zunächst der Aussendurchmesser, um den Mindestdurchmesser für das Rohmaterial zu erhalten, dazu das Bild 18. Blickt man exakt von unten auf den Dodekaeder, so sieht man die Projektion des großen Fünfecks, das sich von Ecke zu Ecke der schräg stehenden Fünfecke spannt. Zieht man um dieses Fünfeck einen Kreis, so umschließt dieser den Dodekaeder vollständig. Es muß also nur der Umkreis des großen Fünfecks bestimmt werden, seine Seitenlänge e wurde vorher schon berechnet (e = 2 * s* sin(54°)). Das dunkelblau eingezeichnete, rechtwinklige Dreieck verfügt über ausreichend Information, um den Radius bestimmen zu können, im Bild unten die schematische Darstellung. Bekannt ist der spitze Winkel innen, er beträgt 72°/2 = 36°. Zudem ist e/2 bekannt, damit ergibt sich RA zu:
(e/2) / RA = sin(36°).
Umgestellt nach RA: RA = (e/2) / sin(36°) und e/2 = s * sin(45°) eingesetzt: RA = s * sin(54°) / sin (36°) Der Mindestmaterialdurchmesser ist 2*RA = 2*s*sin(54°) / sin(36°). Bei 50mm Kantenlänge ergibt sich der Mindestmaterialdurchmeser zu 137.64mm. Nun noch die Höhe des Dodekaeders. Hierzu Bild 19. Betrachtet man die Perspektive, so läßt sich die Gesamthöhe wieder über ein rechtwinkliges Dreieck berechnen, dessen Winkel unten links als Flächenwinkel w bereits berechnet wurde. Die Hypotenuse baut sich aus drei Teilsegmenten auf. Das erste Segment geht von der Mitte der unteren Kante des grünen Fünfecks zur Verbindungslinie der nächsten beiden Ecken. Das zweite Segment vom Ende des ersten Segments zur der unteren Kante gegenüberliegenden Spitze. Nun noch das dritte Segment. Dazu betrachten wir das magentafarbene Fünfeck. Es fehlt zur Höhe noch das Teilstück von der Mitte der horizontalen Verbindungslinie der beiden Ecken bis zur Mitte der oberen Kante. Dieses Teilstück ist auf allen fünf oberen Fünfecken gleich, eines davon liegt exakt dem grünen Fünfeck gegenüber, parallel. Man kann dieses Stück also einfach gedanklich horizontal quer durch den Dodekaeder schieben und an das zweite Teilstück anschließen, seine Länge ist bereits bekannt, es ist genauso lang wie das untere Teilstück. Nun zum unteren Bild, es zeigt die Zusammenhänge: Das erste und dritte Teilstück wurden schon berechnet: h1 = s * cos (18°) Das zweite Teilstück läßt sich ebenfalls leicht berechnen: h2 = s * cos(54°)
Die gesamte Hypotenuse wird damit zu:
H = 2*h1 + h2 = 2*s*cos(18°) + s*cos(54°) s kann ausgeklammert werden: H = s*(2*cos(18°)+cos(54°)
Die Dodekaederhöhe wird damit
DKH = H * sin(w)
mit w = 63,434948823 Grad.
Bei einer Kantenlänge von 50 mm ergibt sich eine Höhe von 111.352 mm.
Damit ist der kurze Ausflug in die Mathematik beendet, er sollte zeigen, daß es an sich recht einfach ist, sich durch solche Körper zu rechnen, es ist etwas fehleranfällig, der CAM-Programmierer braucht sich hierüber keine Gedanken zu machen.
Er sollte sich aber nicht blind auf das Modell verlassen und dessen korrekte Modellierung prüfen. Für eine Kantenlänge von 50mm brauchen wir also ein Materialstück mit einem Durchmesser von mindestens 140mm und einer Länge von rund 115mm.
Im folgenden Abschnitt werden die Überlegungen für die erste Aufspannung durchgeführt.
------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002
|

 erstellt am: 18. Jan. 2011 01:00
erstellt am: 18. Jan. 2011 01:00  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Nein, halt, nicht so schnell.
5. Die Projektverwaltung
Bevor es weitergeht, muß man sich Gedanken über die Projektverwaltung machen. Ist die Projektverwaltung von IV schon ein Kapitel für sich, wird es durch das aufsetzende CAM nicht einfacher und kann sich erst recht zur Zeitbombe entwickeln. Aus einer ipt entsteht bei Inventorcam ein Verzeichnis, Inventorcam erstellt sich wie Solidcam ein Verzeichnis, kopiert sich alle Dateien dorthin und arbeitet mit den Kopien weiter. Man hat 3 Möglichkeiten zu programmieren: 1. Direkt auf die ipt, man verzichtet auf jede weitere Information, benutzt den Mehrseitennullpunkt. Damit weiß man jedoch später nicht mehr, wie das Teil aufgespannt war. 2. Im Zusammenbau, die Spannmittel werden von einem eigenen Verzeichnis aus referenziert. Ändert man die Spannmittel, wirkt sich das auf alle bisher erstellten Programme aus, die diese Teile referenzieren. Das kann auch ins Auge gehen. Vor allem aber kann es schwierig werden, wenn die Serverstruktur geändert werden soll oder man Programme mitnehmen möchte. Pack&go beschränkt sich auf die Inventor-Dateien. 3. Die hier gezeigte Methode ist eine weniger gebräuchliche, das Kryptolaufwerk. Hier erstellt man sich zuerst eine Vorlage, die bereits alle Verzeichnisse und Dateien enthält, die man sich vorbereiten möchte. Die Vorlage kopiert man sich, gibt ihr einen anderen Namen (Teilenummer) und arbeitet mit dieser weiter. Nachteil dieses Verfahrens ist etwas administrativer Aufwand und höherer Speicherplatzbedarf, Vorteil die Vorlage, die man bis zu einem beliebigen Punkt vorbereiten kann und die nahezu beliebige Verschiebbarkeit des ganzen Projektes, ohne daß IV oder Inventorcam das monieren. Nicht geöffnete Projekte sind vor jedem unbeabsichtigten Zugriff sicher. Wie funktioniert es? Das von mir benutzte Programm ist das kostenlose Truecrypt. Zunächst erstellen wir eine Containerdatei mit 100-250MB, nennen sie Vorlage (im Bild links oben), melden diese Datei als Laufwerk Z: an (im Bild links unten), legen dort die nötigen Verzeichnisse an und bauen die Spannmittel für die erste Aufspannung auf, genau so, wie sie auf der Maschine auch sind. Der Baugruppenname 10.iam ist die erste Aufspannung, man nummeriert dann einfach in Zehnerschritten weiter, sollten Zwischenschritte nötig werden, kann man diese dazwischen einfügen. Danach schließt man das Laufwerk wieder, kopiert die Datei Vorlage und benennt sie um, hier wird sie Dodekaeder heissen. Die Vorlagendatei kann beliebig oft kopiert werden, ebenso die Arbeitsdateien (Datensicherung auf Dauer und auch zwischendurch).
Nach dieser kurzen Vorarbeit können wir nun tatsächlich das Rohmaterial definieren.
------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002 C 64
Amiga 1000 mit
8.5 MB RAM und
Seagate ST225
RLL formatiert
|

 erstellt am: 22. Jan. 2011 23:16
erstellt am: 22. Jan. 2011 23:16  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
6. Das Rohteil ableiten
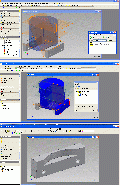
Pic 21 – oben
Im vorliegenden Fall wird die IPT des Werkstücks direkt in das lokale Verzeichnis kopiert, je nach Dynamik der Konstruktion empfiehlt sich diese Trennlinie in der Modellassoziativität. Pic 21 – Mitte Zur Orientierung, welche Fläche die untere ist und bleiben soll, wird der Koordinatenursprung sichtbar geschaltet, liegt die Fläche mangels sorgfältiger Ausrichtung der IPT zum Ursprung nicht wie gewünscht, setzt man einen eigenen Arbeitspunkt. Damit sind zunächst die Vorarbeiten am Werkstück abgeschlossen. Pic 21 – unten Wir rufen eine neue IPT auf, verlassen die Skizze wieder und wählen die abgeleitete Komponente, holen das Werkstück komplett mit allem herein, was es hat.
Pic 22 – oben
Auch in der abgeleiteten Komponente schalten wir uns den Koordinatenursprung sichtbar, damit können danach Werkstück und Rohteil unter Zuhilfenahme zweier Ebenen immer passend zur Deckung gebracht werden. Pic 22 – Mitte Wir wählen eine geeignete Ebene für eine Skizze, hier eignet sich bereits wieder eine Ursprungsebene, um die äusseren Abmessungen des Werkstückes abgreifen zu können. Pic 22 – unten Wir projizieren den Ursprung in die Ebene, den Eckpunkt oben und einen ganz aussen, damit kann ein Rechteck fixiert werden, das den minimalen Materialbedarf festlegt. Pic 23 – oben Für die Bearbeitung muß Material zugegeben werden, oben und unten werden Rechtecke anskizziert, gleiche Breite, die Höhe wird fix bemaßt, hier geben wir oben 2mm zu und unten 12mm. Die Breite des Rechtecks wird bemaßt, was eine getriebene Bemaßung ergibt, die in der Parameterliste „Eckenmass“ genannt wird. Mit dieser wird anhand einer Formel der Rohteilradius berechnet, der mindestens 1mm Aufmaß lässt und in 10mm-Sprüngen den Materialdurchmesser festlegt. IV wählt hier 70mm als Rohteilradius. Pic 23 – Mitte Ein weiteres Rechteck, diesmal längs, für die Materialzugabe rundum. Pic 23 – unten Alle Rechtecke wählen für die Rotation, die innere Linie ist zeitgleich die Achse. ------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002
|

 erstellt am: 22. Jan. 2011 23:19
erstellt am: 22. Jan. 2011 23:19  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Pic 24 – oben Wir erhalten einen Zylinder mit dem nötigen Aufmaß, wählen eine durchsichtige Farbe und legen das Teil mit seinem Namen für die erste Aufspannung im Werkstückverzeichnis ab. Pic 24 – Mitte IV lässt nicht immer, wenn man das möchte, einen Durchgriff durch das Rohteil auf Werkstück zu, man macht sich also eine Extrusion, hier eine Ecke, die man bedarfsweise schnell wegschalten bzw. hinzuschalten kann. Alternativ kann man auch Halb- oder Viertelschnitt in der Zusammenbauumgebung nehmen. Pic 24 – unten Das Rohteil mit der ausgeschnittenen Ecke. Man darf nur nichts an die Flächen dieses Hilfsausschnittes befestigen, weil dieser nur vorübergehend ist.
Pic 25 – oben
Eine neue iam wird geöffent, Rohteil als fixiertes Teil und Werkstück eingefügt. Pic 25 – Mitte Das Werkstück wird zunächst mit dem Arbeitspunkt ans Rohteil gebunden, dann mit zwei Ebenen, hier wieder Ursprungsebenen, die schräge Ebene hilft, die Ausrichtung zu kontrollieren. Pic 25 – unten Im Zusammenbau kann man jetzt mit Doppelklick das Rohteil aktivieren und das Bauteilende entweder vor oder hinter die Hilfsecke setzen.
Pic 26 – oben
Das Werkstück vollständig vom Rohteil umschlossen. Pic 26 – unten Und dasselbe mit der Hilfsecke, die direkten Zugriff auf die Werkstückflächen erlaubt. Sieht man von der Formel ab, mit der IV den Rohteildurchmesser in runden Stufen festlegt, ging alles ohne jegliche Rechnerei, war im Grunde wieder nur CAD-Vorarbeit, die uns hilft, einen schlüssigen Rüstplan zu erhalten. ------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002 C 64
Amiga 1000 mit
8.5 MB RAM und
Seagate ST225
RLL formatiert
|

 erstellt am: 01. Feb. 2011 02:05
erstellt am: 01. Feb. 2011 02:05  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
7. Formbacken für die erste Aufspannung ableiten.
Die Entscheidung für rundes Rohmaterial hat zur Folge, daß man dieses nicht ohne weiteres in einem Maschinenschraubstock aufnehmen kann, weil es kippen wird und u. U. den Fräser beschädigt, entweder man montiert ein Drehbankfutter auf den Maschinentisch, hat passende Prismenbacken. Ist beides nicht der Fall, wird man sich welche machen.
Hier beginnt der Unterschied von CAM zur klassischen Arbeitsweise, die lückenlose Dokumentation einschließlich aller Hilfsmittel, die im Rahmen der Produktfertigung ebenfalls gefertigt werden müssen. Das reine Teileprogramm nutzt später nur wenig, wenn die Spannsituation nicht mehr bekannt ist.
Für solche Sachen legt man sich am besten gleich einen Ordner an, ich nenne ihn „Hilfsmittel“ als Unterschied zu den gekauften Spannmitteln.
Pic 27 oben
Wir öffnen eine neue Zusammenbaudatei, fügen zweimal die rohe Formbacke ein. Im Grunde ein Vierkantmaterial, das schon die beiden Bohrungen zur späteren Befestigung an der Schraubstockgrundbacke besitzt. Als Abhängigkeiten passen wir die beiden Mittelebenen und die Unterseiten, so daß die linke Backe als fixes Teil unbeweglich ist, die rechte sich mit der Maus nun noch verschieben lässt. Pic 27 – Mitte Nun fügen wir noch das vorher abgeleitete Rohmaterial ein, es soll 15mm von oben in den Formbacken aufgenommen werden, mittig sitzen, dazu dienen Ursprungsebenen, hat man keine, macht man sich Arbeitsebenen. Und die fixe Backe soll 5mm – hier als Beispiel – noch überstehen. Pic 27 – unten Ebenso wird auch die lose Backe auf 5mm tangentialem Abstand fixiert. Aufpassen, daß man nicht den Hilfsausschnitt benutzt.
Pic 28 – oben
Diese Baugruppe wird nun in den Hilfsmittel-Ordner abgelegt, man vergibt einen eindeutigen Namen, die Zahl 10 bedeutet, daß es die erste Aufspannung ist. Die Arbeitsschritte in Zehnerschritten zu benennen hat den Vorzug, später noch Zwischenschritte einfügen zu können. Pic 28 – Mitte Wir öffnen eine neue Bauteildatei, verlassen die Skizze, wählen die abgeleitete Komponente und hier den soeben abgespeicherten Zusammenbau, wollen Formbacke1 behalten und den Rest als Differenz abziehen. Benötigt man noch Arbeitsebenen, kann man diese in der Rubrik „Andere“ wählen, da aber alles in diesem Zusammenbau an den Ursprungsebenen brauchbar ausgerichtet ist, ist auch keine weitere Auswahl mehr nötig.
Pic 28 – unten
Die verbleibende Formbacke. Da wir beim Rohmaterial damit rechnen müssen, daß das nicht ganz exakt ist, kann es passieren, daß es trotz der Rundung wieder nur an der mittleren Kante anliegen und doch wieder kippen würde. Wir müssen also prismatische Anlageflächen schaffen. Pic 29 – oben Auf die Backenoberseite kommt eine Skizze, die in etwa das auszusparende Trapez darstellt und eine zur Backenvorderseite parallele Linie, an deren Endpunkten das Material später theoretisch anliegen soll. Pic 29 – Mitte Diese Anlagepunkte sollen hier 5mm von der Vorderkante entfernt sein, wir bemaßen die Linie, sie ist damit fixiert. Pic 29 – unten Nun skizzieren wir zwei Linien vom Zentrum des Kreises zu den Endpunkten der Linien, legen die Schrägen koinzident und lotrecht an die Endpunkte. Vorne stellen wir nun die Formbacke noch frei, lassen 3mm Material stehen, geben also dieses Maß an.
------------------
-
Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002
|

 erstellt am: 01. Feb. 2011 02:08
erstellt am: 01. Feb. 2011 02:08  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
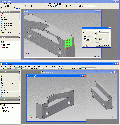
Pic 30 oben Da die entstandenen Innenecken nicht gefräst werden können, müssen sie verrundet werden, das CAM würde das auch selbst tun, aber wir möchten den Fräser ein wenig sanfter führen, geben einen Radius an, der zu einer kurzen Bogenfahrt zwingt. Das ist bei manuellen Programmierern nicht gern gesehen, im CAM spielt es keine Rolle und schont Werkzeug und Maschine. Pic 30 – Mitte Dasselbe Spiel wiederholen wir jetzt für die Backe, die an die bewegliche Schraubstockgrundbacke kommen wird. Also wieder eine neue ipt, die Skizze verlassen, eine abgeleitete Komponente des letzten Zusammenbaus und jetzt von der anderen Formbacke alles abziehen.
Pic 30 – unten
Auch die kann man nicht so lassen, sie soll eine gerade Anlagefläche als dritte Linie bilden, wir fräsen sie also gerade ab. Dazu an eine Stirnseite eine Skizze und den Kreisbogen projizieren.
Pic 31 – oben Ein Rechteck skizziert, es ist durch die projizierte Linie und die Ecke fixiert, es kann quer durchextrudiert werden. Pic 31 – unten Die beiden Formbacken, die nun in den Schraubstock eingebaut werden und als erstes dann tatsächlich auch gefertigt werden können.
------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002 C 64
Amiga 1000 mit
8.5 MB RAM und
Seagate ST225
RLL formatiert
|

 erstellt am: 02. Feb. 2011 02:14
erstellt am: 02. Feb. 2011 02:14  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
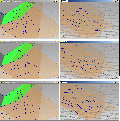
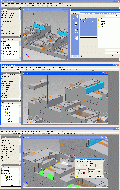
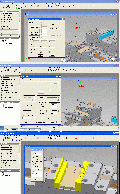
8. Die Spannbacken einbauen und programmierenNachdem die Spannbacken nun bereitstehen, können sie mit den Schraubstockbacken verknüpft und auch programmiert werden. Pic 32 – oben Wir rufen den in der Vorlagendatei schon vorbereiteten Zusammenbau auf, ich selbst mache bei den Aufspannungen Zehnerstufen, die erste ist also 10.iam. Pic 32 – Mitte Da wir die Leisten nicht brauchen, werden sie gelöscht, die fixe Backe in den Zusammenbau geholt und … Pic 32 – unten … in der Realität auch eingebaut. Pic 33 – oben Dasselbe machen wir auch mit der losen Schraubstockbacke. Die Schrauben selbst brauchen wir nicht, sie können aber durchaus für Kollisionsanalysen von Interesse sein. Pic 33 – Mitte Die lose Backe muß auf eine definierte Stellung und der Schraubstock für diese Aktion auch gespannt, man legt also ein Zwischenstück ein und spannt dieses. Einen Klotz mit Beschriftung legt man sich gleich in der Vorlagendatei bereit, so daß er ggf. nur noch in der Größe angepasst werden muß, IV ändert dann auch die Beschriftung passend mit. Pic 33 – unten Und jetzt wird das CAM aus dem CAD heraus gestartet. Pic 34 – oben Das CAM fragt anfangs ein paar Daten ab, allen voran die Verzeichnisse. In neueren Versionen is dieser Dialog geschickter gestaltet, ich umgehe das Problem der ständigen Anpassung des Arbeitsverzeichnisses ohnehin mit dem Kryptocontainer, kann also die von mir voreingestellte Angabe des Laufwerks Z stehen lassen, es geht mit OK weiter. Pic 34 – Mitte Egal, welches CAD als Unterbau dient, dieses CAM kopiert sich alle Dateien in ein eigenes Unterverzeichnis und arbeitet mit diesen weiter, es hat sich das Verzeichnis „10“ für die erste Aufspannung im Laufwerk Z angelegt und dort die Arbeitsdateien hineinkopiert. Synchronisiert man später bei Änderung des Originalwerkstücks, werden die Kopien überschrieben, hat man sich dort jedoch Skizzen für Werkzeugwege angelegt, sind die danach weg. Man muß also ein waches Auge darauf haben, daß man Arbeitsgeometrie sich immer in der richtigen Ebene anlegt. Pic 34 – unten Bei der Festlegung des Nullpunkts oder der Nullpunkte gibt es verschiedene Konzepte, ich benutze das weniger gebräuchliche, das einen fixen Nullpunkt im Raum vorsieht. Dafür brauche ich nur auf seine obere Fläche zu klicken und habe den Usprung, die Achsenrichtungen und auch obere und untere Arbeitsraumbegrenzungen gewählt. Alles oberhalb dieses Nullpunks wird im Eilgang verfahren, dort darf nichts im Wege stehen, also keine Spannzwingen oder Schraubenköpfe. Der CAM-Nullpunkt wird jetzt nur mit den dünnen Linien an der oberen Fläche dieses Hilfsteils angezeigt, die Farben sind RGB für XYZ.
------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002
|

 erstellt am: 02. Feb. 2011 02:16
erstellt am: 02. Feb. 2011 02:16  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
Pic 35 – oben Mit dem fixen Nullpunkt hat das CAM alle Ebenen übernommen, man klickt sich also gleich weiter. Pic 35 – Mitte Wieder zurück im Anfangsdialog ist jetzt der Koordinantenindikator am Nullpunkt, man wählt die Steuerung, die man nachträglich ändern kann. Hier soll es Fanuc sein. Pic 35 – unten Für die Simulation wählt man noch Roh- und Fertigteil, hier nur der Ordnung wegen gemacht, beim Dodekaeder wird es von Bedeutung sein. Die gewählten Teile werden hier gelb dargestellt.
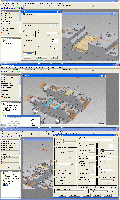
Pic 36 – oben
Damit ist dieser formale Teil abgeschlossen, das Material kann man wählen, wenn man auch die Schnittdatenbank nutzen möchte, meist wird man jedoch fixe Schnittwerte gleich an die Werkzeuge binden. Pic 36 – Mitte Rechtsklick auf Jobs, ein Profiljob soll es werden, er fährt an Geometrie entlang. Pic 36 – unten In meiner alten Programmversion sind die Dialogboxen noch groß, man füllt sie einfach aus, in neueren Versionen sind es einzelne Blätter, im Grunde dasselbe. Hier arbeitet man sich einfach spaltenweise durch. Pic 37 – oben Zuerst die Auswahl der Geometrie, die zu bearbeiten ist, die V-förmige Aussparung ist die erste Kontur. Die Richtung ist für Gleichlauf. Pic 37 – Mitte Ebenso wird die Kontur des Absatzes für die lose Backe gewählt. Pic 37 – unten Und ein Fräser mit 16mm Durchmesser, vier Schneiden aus dem Werkzeugkatalog gewählt. Mit dieser Auswahl sind Drehzahl und Vorschub bereits mit gewählt, ebenso der Magazinplatz, der später in der Maschine auch mit diesem Werkzeug bestückt sein muß.
Ich selbst lege die realen Geometriemaße der Werkzeuge im CAM ab. ------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
murphy2
Ehrenmitglied
-
    
   Beiträge: 1726
Registriert: 30.07.2002 C 64
Amiga 1000 mit
8.5 MB RAM und
Seagate ST225
RLL formatiert
|

 erstellt am: 02. Feb. 2011 02:18
erstellt am: 02. Feb. 2011 02:18  <-- editieren / zitieren --> <-- editieren / zitieren -->   Unities abgeben: Unities abgeben:          
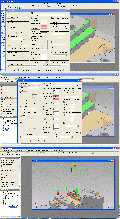
Pic 38 – oben Nun die mittlere Spalte der Dialogbox, die Z-Ebenen, die obere Job-Ebene is die obere Fläche der Spannbacken, die untere die untere grün markierte Ebene. Rot hinterlegte Zahlen in den Diaologboxen bedeuten, daß diese Maße Modelländerungen mitmachen. Pic 38 – Mitte Die Aussparungen sollen geschruppt werden und dann in einem Schnitt geschlichtet, die Werte in die Dialogbox eingetragen, neuere Programmversionen haben noch ein paar Optionen mehr. Als An- und Abfahrstrategie soll tangential angefahren werden, 20mm ergeben einen ausreichenden Sicherheitsabstand. Pic 38 – unten Und so sehen die Fahrwege aus, in Z heillos zuviel, man ruft den Job noch mal auf, ändert die Rückzugsebene und das Schruppen, daß beim Schruppen Gleich- und Gegenlauf gemischt werden dürfen.
Pic 39 – oben
Das sieht dann schon besser aus.
Pic 39 – unten
Nun lässt man sich das Programm rechnen, es durchläuft den sog. Postprozessor, schreibt einen Programmkopf mit allen wichtigen Maschinenvoreinstellungen, wie man es im Postprozessor festgelegt hat und danach das Programm. Wichtig ist aber eine Kleinigkeit, die Simulation war vor dem Postprozessorlauf, das Programm danach. Daher sollte man bei Änderungen am Postprozessor – im Grunde eine rudimentäre Programmiersprache – in etwa wissen, was man tut. Man hat bis jetzt also im Grunde nichts rechnen müssen.
Damit ist die erte Aktion abgeschlossen, das Rohteil des Dodekaeder kann seine erste Bearbeitung erfahren.
------------------
- Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP |
| Anzeige.:
Anzeige: (Infos zum Werbeplatz >>)
 |

 Foren auf CAD.de
Foren auf CAD.de

 Inventor CAM
Inventor CAM

 Der Cylindro-Pentagon-Dodekaeder
Der Cylindro-Pentagon-Dodekaeder

![]()






















 Aussparungen.
Aussparungen.