---

Picture1.jpg

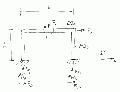
Hallo zusammen,

habe nachfolgendes Problem. Ich habe einen beidseitig fest eingespannten Rahmen (siehe Bild) mit unterschiedlichen Belastungen (Moment M und Kraft Fy mittig angreifend, Kraft Fx seitlich angreifend). Riegel und Steg haben unterschiedliche Steifigkeiten.

Ich möchte den Biegemomentverlauf entlang des Balkens bestimmen. Da es sich um ein dreifach statisch unbestimmtes System handelt habe ich versucht mit dem Satz von Castilganio zu arbeiten und mir erstmal die statisch unbestimmten zu ermitteln. Leider ohne Erfolg.  

Mein Ziel ist es wie bei den Rahmenformeln eine einfache handhabbare Gleichung für diesen Belastungsfall zu bekommen, in die ich nur noch meine bekannten Belastungen und Abmessungen einsetzen muss, damit ich mir die Biegemomente an bestimmten Stellen ermitteln kann.

Frage: Wie würdet Ihr dieses Problem lösen => würde mich über eine Beschreibung der Vorgehensweise und angewendeten Methoden, Lösungsverfahren freuen. Wenn natürlich jemand den Ehrgeiz hat, dass Problem formelmäßig zu lösen und zur Verfügung zu stellen wäre ich auch nicht abgeneigt.

Ich habe bisher nur die Rahmenformel für den Querkraftbelasteten Riegel zur Verfügung. Gibt es die Rahmenformel auch für

a) Eine mittig angreifende Einzelkraft am Riegel Fy
b) ein mittig angreifendes Moment am Riegel M
c) eine angreifende Kraft am Steg Fx

Meine Idee ist es, diese 3 Einzelfälle zu berechnen und zu superpositionieren. Damit hätte ich ja auch wieder meinen gesuchten Belastungsfall und könnte mir die Lagerreaktion und die Biegemomente bestimmen.

Mit freundlichen Grüßen und vorab vielen Dank

Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP

---

Zitat:

---

Original erstellt von mrkw01:

Meine Idee ist es, diese 3 Einzelfälle zu berechnen und zu superpositionieren. Damit hätte ich ja auch wieder meinen gesuchten Belastungsfall und könnte mir die Lagerreaktion und die Biegemomente bestimmen.

---

So ein 'Tor' ist ja eine typische Übungaufgabe. Verschiedene Varianten finden sich in jedem weiterführenden Mechanikbuch. Mein Ergeiz solche Aufgaben zu lösen ist folglich relativ gering. 

Anstatt die drei Fälle einzeln zu betrachten, ist es nicht viel mehr Arbeit von Vorn herein mit allen Kräften zu rechnen. Das Endergebnis wird nicht anders aussehen.

"Einfach handzuhaben" im Sinne von "Per Excel Darstellbar" ist jedenfalls möglich. Je nach späterem Anwenderkreis ist eine Plausibilitätsprüfung von Eingaben zwingend anzuraten! ( Meine Erfahrung bei Erstellung von Kalkulationstabellen für den Vertrieb...Geh vom Schlimmsten aus!    )

Mit einem halbwegs gescheiden Taschenrechner oder Mathe-Programm begleitet, bleibt die Arbeit/Fehleranfälligkeit in Grenzen.

An welcher Stelle scheitert denn deine Berechnung?

Ansonsten: FEM :P

Grüße,

Jörg

------------------

Die größtmögliche Geschwindigkeit ist die Dunkelgeschwindigkeit, denn so sehr sich das Licht auch anstrengt, die Dunkelheit war schon vorher da.

Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP

---

Danke für deine Antwort.

„Typische Übungsaufgabe“, das habe ich auch erst gedacht, ich wurde bis jetzt aber eines besseren belehrt. Ich weiß nicht wo mein Fehler ist. Ich bekomme ganz wilde Formeln mit zahlreichen Brüchen und Termen. Es hebt sich nichts auf oder kürzt sich weg. Letztendlich lassen sich auch die statisch unbestimmten dadurch nicht beseitigen. Ich verzweifle langsam. Habe schon drei Anläufe genommen. Habe auch versucht erstmal nur mit einer Belastung zu rechnen. Hier habe ich die gleichen Probleme.

FEM kommt erstmal nicht in Frage, soll ja Bestandteil eines handhabbaren Tools in Excel werden. Diejenigen, die es benutzen sollen bzw. müssen haben nur Excel.

Weil die Berechnung über den geplanten Weg gescheitert ist, habe ich mir gedacht ich könnte die Rahmenformeln verwenden, wenn es diese für die drei Einzelfälle geben würde. Habe bei meiner Recherche bisher nur die mit einer Streckenlast belastete Rahmenformel gefunden. Vielleicht kennt ja jemand eine Internetseite wo evtl. verschiedene Rahmen mit unterschiedlichen Belastungen samt Lösungsformeln aufgeführt sind.

Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP

---

Hmmmmmm... Latsch mal in die Bibliothek und schau dir die weiterführende Mechanik Bücher an.

Ich bin mir absolut sicher die Verschiebung verschiedenst belasteter dreifach überbestimmter Tore schon mehrfach gesehen zu haben und bei meiner Mechanik I Klausur kam sogar eins dran.

Rahmenformeln sind IMHO zu stark vereinfacht ( ist zB der Querschnitt nicht konstankt, sind sie schon nicht mehr verwendbar ) und ob die Superposition anschliessend ein richtiges Ergebnis liefert weiss ich gerade auch nicht, weil ich die theorie hinter den Formeln nie betrachtet habe. Die würde ich vorher umbedingt prüfen und schon bist wieder bei Castigliano gelandet...

Grüße,

Jörg

------------------

Die größtmögliche Geschwindigkeit ist die Dunkelgeschwindigkeit, denn so sehr sich das Licht auch anstrengt, die Dunkelheit war schon vorher da.

Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP

---

01.JPG 02.JPG

Danke Jörg, für deine Unterstützung bzw. Ratschläge.

So habe jetzt noch mal Literaturstudium betrieben. Einen Fehler habe ich gefunden, den ich bei der Anwendung des Satzes von Castigliano gemacht habe. Laut Literatur sind die 3 statisch unbestimmten zu wählen und damit dürfen die anderen Lagerkräfte und Momente im Momentverlauf nicht vorkommen. Darauf habe ich bisher nicht 100%ig geachtet. Quelle: http://books.google.de/books?i  d=S3wKf_da7tcC&pg=PA417&dq=satz+von+castigliano&client=firefox-a&cd=1#v=onepage&q=satz%20von%20castigliano&f=false  (Seite 417, ca. Mitte)

Habe jetzt angefangen noch mal zu rechnen (siehe Bild). Jedoch tritt hier bereits beim ersten Teilreich das Problem auf, dass das Moment (hier MB) immer noch im Momentenverlauf vorhanden ist. Dadurch, dass es in Gleichung III nur zusammen mit MA auftritt bekomme ich es auch nicht weg.

Gibt es eine Möglichkeit das MB zu eliminieren bzw. aus den erlaubten Größen darzustellen   ?

edit: habe noch die anderen Teilbereiche angehangen. In jedem Ausdruck ist noch MB drinne.

[Diese Nachricht wurde von mrkw01 am 06. Jan. 2010 editiert.]

[Diese Nachricht wurde von mrkw01 am 06. Jan. 2010 editiert.]

Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP

---

Hallo,

Also das Google-Buch reicht nicht komplett aus...

Mach es dir einfacher und fang mit einem dreiwertiges Lager an einer Seite an.

Dann probiere aus ob du es mit einem einfach unbestimmten Fall hin bekommst. ( Bin ich mir sicher  )

Danach die anderen beiden verbleiben einfach unbestimmten Fälle und ein Buch in dem das Verfahren ordentlich erklärt wird und vorallem die extremst hilfreichen Tabelle der Integrale für die Momentenverläufe enthällt und; Tadaaaa!

Wünsche viel Spaß beim finden der Lösung!

Grüße,

Jörg

------------------

Die größtmögliche Geschwindigkeit ist die Dunkelgeschwindigkeit, denn so sehr sich das Licht auch anstrengt, die Dunkelheit war schon vorher da.

Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP

---

Hallo,
das sollte eigentlich nicht schwer zu berechnen sein, ich probier's mal.

Eine Antwort auf diesen Beitrag verfassen (mit Zitat/Zitat des Beitrags) IP